One morning last week, as I sat in my armchair reading the report of the Lessons Learnt and Reconciliations Commission (LLRC), I saw a man dressed only in a sarong running along the road just outside my house. You might think there is nothing unusual about a man in a sarong running – perhaps he is running to catch a bus or is being chased by a dog. That might be so, if I saw this running man in Sri Lanka. But no, this is one freezing winter morning in BridgeTown, UK, where the probability of a seeing a man running in his sarong is infinitesimally small. Remember the story about someone famous jumping out of the bath-tub and running naked on the road shouting “Eureka”? My story today is something in the same spirit.
The man I saw is a friend. His name is Accuratus Numeratus, with origins in Jaffna, Sri Lanka. He earns a living by extracting useful information from large and complex datasets. Naturally, the contentious issue of how many Sri Lankans actually perished during the last phases of the war intrigued him. We know all sorts of numbers are quoted by those with their individual agendas, estimates ranging from zero to 40,000 – a massive range indeed. So, this man Numeratus set about carrying out a computational way of figuring this out. The steps of such an approach are known to all of us, even the non-experts like you and I. Formulate a model, collect some data from a small sample and extrapolate to see if the model fits the data.
The Model: Man is a social animal, it is said. Margaret Thatcher, the former Prime Minister of the UK, is perhaps the best known evil person who didn’t believe in this. She said there is no such thing as society, just a collection of individuals. Naturally, if you claim something does not exist, you have to destroy it to prove your point, don’t you? Thatcher is known to have done that in style. But unlike her, we know we are a well linked society. We are linked so well that the average distance between two of us taken at random is six hops. I can start from myself and go “I know X”, “X knows Y”, “Y knows Z” etc… and in six hops I can reach President Obama. Note this is average results, estimated across all pairs of individuals, not the distance between every pair of individuals. So, Numeratus theorized that the Tamil community could be modelled as a network, linked in the same way as a network in which the average distance between two random nodes is six. (There are other properties of the statistics of connectivity which I avoid detailing in this forum.)
The Data: Whenever he got a chance, Numeratus collected data. From his relatives and arbitrary people he met at weddings, funerals and conferences, he would gently ask: “Did anyone directly known to you get killed in the Vanni?” “Do you know anyone who knows anyone who got killed in the Vanni?” The answers he meticulously recorded in his little notebook, giving each person an imaginative nickname to hide their identities, yet avoiding duplication. (If only his relative knew these nicknames, my friend’s days will be numbered, for sure.)
Numeratus then set about doing the following calculation. Start from a big network of 300,000 nodes, connected as explained before, and see how many nodes you ought to take out at random before the results explained the data you have collected. You have to do this again and again (known in jargonese as Monte Carlo simulations) to make the results meaningful, so Numeratus wrote some software and ran it on a big computer, over several weeks.
The answer surprised him, a totally counter-intuitive small number, with huge margin of error, is what he found. “No way,” he said to himself, “if you have such a large number of people packed in a small area and blast them with a few rounds of shells from a distance, the loss should be much bigger than what my calculations reveal.” He re-visits his computer code several times looking for bugs, turns the computer off and on several times – as any computer expert would do on such occasions — and re-runs the programme. Nothing changes. A counter-intuitive result is all he has.
After months of frustration with this problem, Numeratus remembered something very basic that Lakshman Jayatillake had taught him during thermodynamics lessons at HillTop University. “Your challenge is to build simple (parsimonious) models, making sensible assumptions about the problem domain,” Jayatillake had drilled into his students, “but you must always perform sanity checks — if the answer doesn’t make sense, never be afraid to question the assumptions upon which your model was based. Learning begins when you question your assumptions.”
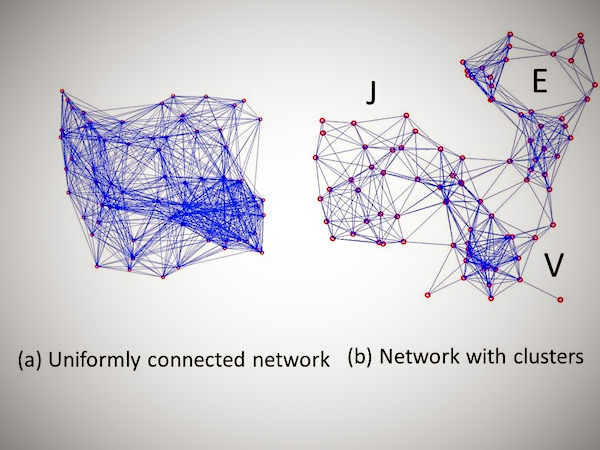
When Numeratus questioned his assumptions, it suddenly dawned on him. “Of course,” he shouted, “it is not a uniformly connected network – the stuff comes in clusters.” His is a profound error. You will see this from the illustration I provide below, that in such clustered networks, you cannot learn much lessons about one part by querying another.
Returning from the run in his sarong on that cold winter morning, Numeratus made an entry in his log book about the lesson he learnt — using a hybrid of mathematical and amateur poetic forms. Such is the power of mathematics that once you find an accurate formulation, including proper notation, the solution will stare at you and pop out of the page. There remains no need to spell it out.
The Alphabet Song of Lessons Learnt
by Accuratus Numeratus
Oh my glorious land, my Island:
The letter L,
Thy short sighted politics, the hegemony:
Of letter S,
Rebellion in response, or plain selfish arrogance:
Of letter J,
Warlord’s ammunition, sacrificial little lambs the poor:
Of letter E,
On that long march to massacre, in the backyards:
Of letter V.